Probability of Multiple
Events
The Venn Diagram as a Tool
Venn diagrams can be used as a tool to help breakdown
problems
of multiple events into much simpler problems. For instance:
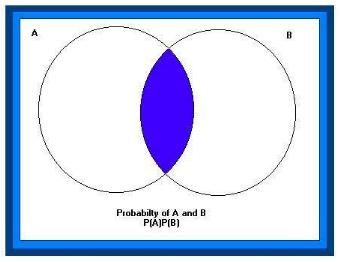
The probability of A and B can be
by this Venn. This
help you to see that to get this
we will need to find only what
things belong to both. To do this, we multiply the probability of A
by the
of B. Mathematically it looks like this:
P(A and B) = P(A)P(B)

The probability of A or B can be represented
by this Venn.
This helps you to see that to get this probability we will need to take
away the parts that the two events share. So A and B needs to be added
together and the we need to take away the part that A and B shares. Mathematically
this means:
P(A or B)=P(A)+P(B)-P(A
and B)
If we combine the two basic ideas illustrated
above with the basic
definition
of probability:
If we combine the two basic ideas illustrated
above with the basic
# of times a specific event occurs
# of total events in the group
we can tackle more complicated
probabilities with even more events.
Try to solve the following probability problem using the Venn diagram worksheet
provided.
Venn Worksheet
Problem:
A high school is offering three languages: one in Spanish, one
in French, and one in German. These classes are open to any of the
100 students in the school. There are 28 students in the Spanish class,
26 in the French class, and 16 in the German class. There are 12 students
that are in both Spanish and French, 4 that are in both Spanish and German,
and 6 that are in both French and German. In addition there are 2 students
taking all three classes.
(a) If a student is chosen randomly, what is the
that he
or she is taking exactly one language class?
(b) If a student is chosen randomly, what is the
that he or she
is taking exactly one language class?
Strategies Home

